计算机组成原理笔记(二)
三、运算器
1.定点加减法运算
①运算原理
运算公式
- 补码加法:$ [x]_b+[y]_b=[x+y]_b\quad(mod\enspace M) $
- 补码减法:$ [x-y]_b=[x]_b+[-y]_b=[x]_b-[y]_b\quad(mod\enspace M) $
- 对于定点小数,$ M=2 $;
- 对于定点整数,$ M=2^{n+1} $,其中$ n $为不包含符号位的位数。
运算规则
- 操作数采用补码表示,符号位参加运算;
- 运算结果为补码,符号位的进位位(模)直接丢弃。
溢出判断
单符号判断法:利用操作数和运算结果的符号位进行判断
设$ X_f $,$ Y_f $为运算操作数的符号位,$ S_f $为运算结果的符号位,$ V $为溢出标志位,当$ V=1 $时表示发生溢出
加法溢出规则:“正正得负,负负得正”
$ V=X_fY_f\overline{S_f}+\overline{X_f}\enspace \overline{Y_f}S_f $减法溢出规则:“正负得负,负正得正”
$ V=X_f\overline{Y_f}\enspace \overline{S_f}+\overline{X_f}Y_fS_f $
进位位判断法:符号位进位和最高数据位进位进行异或操作
- 设运算时最高有效数据位产生的进位信号为$ C_d $,符号位产生的进位信号为$ C_f $,溢出检测逻辑表达式为$ V=C_f\oplus C_d $
- 对于加减法均适用
双符号判断法
- 根据变形补码中双符号位的定义,可以得到,当符号位为$ 01 $或$ 10 $时发生溢出;
- 溢出检测逻辑表达式公式为$ V=S_{f_1}\oplus S_{f_2} $
- 将双符号运算结果的两个符号位进行异或操作
②一位全加器$ FA $($ Full\enspace Adder $,一个带进位的一位加法器)
计算原理
- $ S_i=X_i\oplus Y_i\oplus C_i $;
- $ C_{i+1}=X_iY_i+(X_i+Y_i)C_i\quad \Delta2T $;
- $ C_{i+1}=X_iY_i+(X_i\oplus Y_i)C_i\quad \Delta5T $
逻辑实现

③多位串行加法器($ Ripple\enspace Carry\enspace Adder $,行波进位加法器)
对$ n $位串行进位加法器进行简单的改造即可得到$ n $位的加法电路;
无符号溢出为$ C_n $,有符号溢出为$ overflow=C_n\oplus C_{n-1} $;
计算原理
- $ C_n\quad \Delta(2n+3)T $
- $ S_{n-1}\quad \Delta(2n+4)T $
- $ overflow\quad \Delta(2n+6)T $
逻辑实现
当采用多位串行加法器进行减法运算时,需要将减数的补码送入加法器。
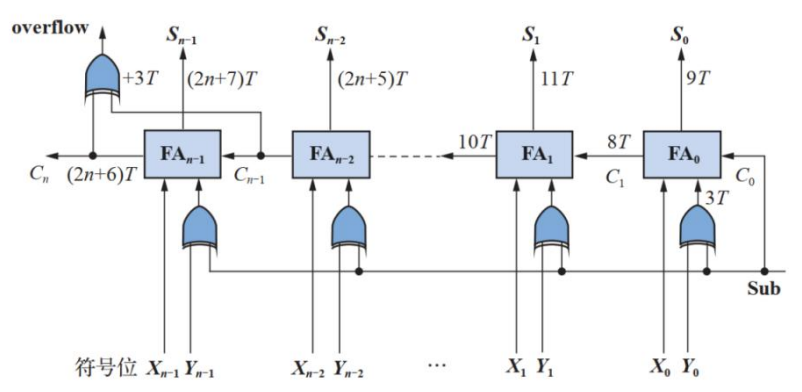
④可控加减法电路($ Controlled\enspace Adder/Subtractor $)
在$ n $位串行加法器的基础上引入$ sub $信号;
- $ sub $信号为$ 1 $时表示进行减法,$ sub $信号为$ 0 $时表示进行加法;
计算原理
数据位为$ Y_i'=Y_i\oplus sub $
最低位的进位输入为$ sub $
逻辑实现
⑤先行进位加法器($ Carry\enspace Look-Ahead\enspace Adder $)
计算原理
设进位生成函数:$ G_i=X_iY_i $,进位传递函数:$ P_i=X_i\oplus Y_i $
由$ S_i=X_i\oplus Y_i\oplus C_i $,$ C_{i+1}=X_iY_i+(X_i\oplus Y_i)C_i $可得
$ S_i=P_i\oplus C_i $,$ C_{i+1}=G_i+P_iC_i $进位信号仅与$ G $,$ P $,$ C_0 $有关:
$ C_n=G_{n-1}+P_{n-1}G_{n-2}+P_{n-1}P_{n-2}G_{n-3}+\cdots+P_{n-1}P_{n-2}\cdots P_1P_0C_0 $成组进位生成函数:$ G^*=G_{n-1}+P_{n-1}G_{n-2}+P_{n-1}P_{n-2}G_{n-3}+\cdots+P_{n-1}P_{n-2}\cdots G_0 $
成组进位传递函数:$ P^*=P_{n-1}P_{n-2}\cdots P_0 $
- $ C_n=G^*+P^*C_0 $与$ C_1=G_0+P_0C_0 $拥有相同的形式,即$ 4 $位一组的进位信号可以采用相似的原理组成成组的先行进位,便于级联操作。
逻辑实现($ 4 $位先行进位电路,$ CLA $)
- $ 4 $位先行进位电路的总延迟为$ 2T $
逻辑实现(四位快速加法器)
- 利用$ CLA $实现的四位快速加法器总延迟为$ 8T $;
- 而串行加法器的时间延迟$ (2n+4)T=12T $,相比之下性能提升$ 1.5 $倍。
逻辑实现($ 16 $位组内并行、组间串行加法器)
关键延迟为$ 14T $,相比串行的$ (2n+4)T=36T $,性能提升$ 2.6 $倍。
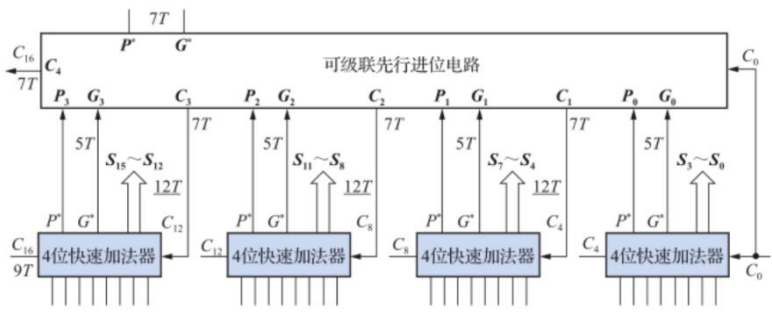
逻辑实现($ 16 $位组内、组间并行加法器)
- 将$ G^* $和$ P^* $送至可级联先行进位电路$ (2T) $,实现组间并行;
- 延迟为$ 12T $,相比串行加法器的时间延迟$ (2n+4)T=36T $,性能提升$ 3 $倍。
2.定点乘法运算
(1)原码一位乘法
符号位运算规则:符号位单独运算,乘积符号位等于乘数和被乘数符号的异或;
数值位运算规则:采用绝对值进行运算,设数值位长度为$ n $,如下图所示:
可见,乘法可由加法实现,存在的问题:
需要多输入的全加器
需要长度为$ 2n $的积寄存器
对应乘数的不同位,部分积左移次数不同,且乘法过程中总移位次数多
运算改进方法:
采用基于一位全加器$ FA $的循环累加$ 0 $或者被乘数
从部分积和乘数寄存器取结果
每次进行累加时,右移部分积,同时右移乘数寄存器,将部分积移出位送入乘数寄存器高位,即将{部分积,乘数寄存器}组合后一起算数右移
由于原码一位乘法中,符号位不参与运算,因此这里的算术右移操作是指将进位位作为算术右移后的最高位
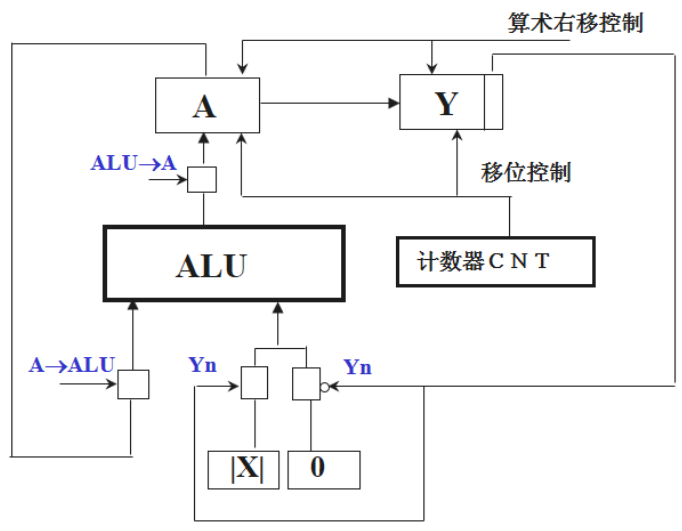
改进后的运算公式:
- $ \{P,y\}=\{(P+y_n\vert x\vert),y\}/2 $
部分积$ P $的初值为零,每次将部分积$ P $累加上$ y_n\vert \vert $后连同数据$ y $一起同步算术右移得到新的部分积,一共要进行$ n $次运算和移位操作,最终的$ 2n $位乘积存放在$ P $和$ y $两个寄存器中。
逻辑左移:数据整体左移一位,最高位$ D_{15} $被移出至$ CF $,最低位$ D_1 $补$ 0 $;
算术左移:数据整体左移一位,最高位$ D_{15} $被移动,最低位$ D_1 $补$ 0 $;
逻辑右移:数据整体右移一位,最高位$ D_{15} $补$ 0 $,最低位$ D_1 $被移出;
算术右移:数据整体右移一位,最高位$ D_{15} $填补符号位,最低位$ D_1 $被移出。
逻辑表示:
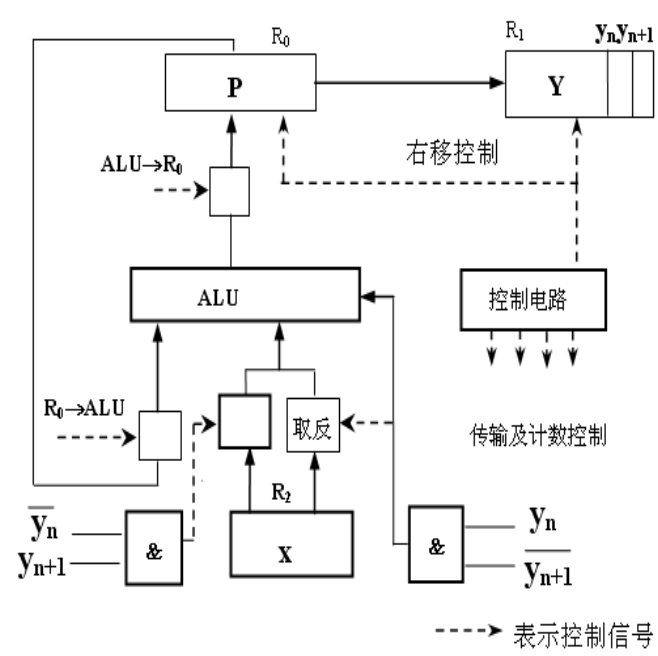
(2)补码一位乘法
运算规则:
补码一位乘法中符号位参加运算,乘数取单符号位;
具体运算公式:$ \{P,y\}=\{(P+(y_{n+1}-y_n)[x]_b,y\}/2 $;
在数据末位增加一位附加位$ y_{n+1}=0 $,部分积$ P $初值为$ 0 $
当$ Y_nY_{n+1}=00 $或$ 11 $时,部分积加$ 0 $
当$ Y_nY_{n+1}=01 $时,部分积加$ [x]_b $
当$ Y_nY_{n+1}=10 $时,部分积加$ [-x]_b $
每次部分积计算完毕后连同乘数$ y $一起同步算术右移一位
由于补码一位乘法中,符号位参与运算,因此这里的算术右移操作是指将符号位作为算术右移后的最高位
由于符号位参与了运算,累加运算需要进行$ n+1 $次,但移位次数只需要进行$ n $次
逻辑表示:
(3)阵列乘法器
①横向进位原码阵列乘法电路
 $ n $位的阵列乘法器需要$ n(n-1) $个全加器,时间延迟为$ [n+2(n-2)]*3T+T=(3n-4)*3T+T. $
$ n $位的阵列乘法器需要$ n(n-1) $个全加器,时间延迟为$ [n+2(n-2)]*3T+T=(3n-4)*3T+T. $
②斜向进位原码阵列乘法电路
 $ n $位的阵列乘法器需要$ n(n-1) $个全加器,时间延迟为$ 2*(n-1)*3T+T=(2n-2)*3T+T. $
$ n $位的阵列乘法器需要$ n(n-1) $个全加器,时间延迟为$ 2*(n-1)*3T+T=(2n-2)*3T+T. $
③原码阵列乘法器

④补码阵列乘法器

⑤阵列乘法器流水线

3.浮点运算
阶码和尾数采用补码表示的浮点数加减运算
运算概述
设有两个浮点数$ X=2^m\times M_x $,$ Y=2^n\times M_y $
当$ m=n $时,尾数部分直接运算即可得到浮点形式的运算结果;
当$ m\ne n $时,需要使二者阶码相等后再行尾数部分的运算,称为对阶;
尾数的计算结果可能不满足规格化,需要进行规格化处理。
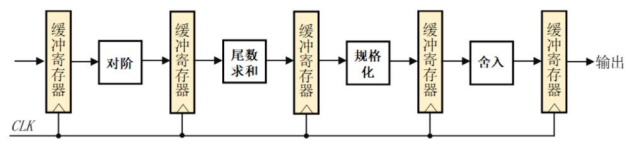
运算过程
对阶(小阶向大阶看齐)
- 求阶差:对阶码进行减法运算,得到阶码的差值
- 阶码的调整与尾数的移位:将阶码较小的浮点数的尾数右移$ m-n $位
尾数运算(进行定点运算)
- 按照定点数的补码加减法运算执行尾数加减操作
规格化运算结果,需要规格化时进行左规或右规操作
- 为了处理方便,让尾数的符号位扩展成双符号位
- 当运算结果为$ 11.0\cdots\cdots $或者$ 00.1\cdots\cdots $的形式时为规格化数
- 非规格化处理
- 当运算结果为$ 10.\cdots\cdots $或者$ 01.\cdots\cdots $的形式时发生上溢,将尾数右移一位,并将结果的阶码加1;
- 当运算结果为$ 11.1\cdots\cdots $或者$ 00.0\cdots\cdots $的形式时,需要左规格化,尾数连同符号位一起左移,直到出现$ 11.0\cdots\cdots $或者$ 00.1\cdots\cdots $的形式时结束,左移多少位阶码就减多少。
舍入处理
- 末位恒置$ 1 $法:只要因为移位丢失的位中有一位为$ 1 $,便在运算结果最低位加$ 1 $;
- $ 0 $舍$ 1 $入法:当丢失位数的最高位为$ 1 $时在运算结果最低位加$ 1 $;
- 舍入后可能还需要进行二次规格化
溢出判断
- 阶码溢出时浮点数才会发生溢出
- $ IEEE754 $浮点数加减运算
对阶和规格化过程中,阶码运算采用移码加减法运算规则;
尾数的运算采用原码运算规则,且隐藏位要参与运算;
规格化过程
- 若尾数形式为$ 1.\cdots\cdots $,则为规格化尾数;
- 若尾数形式为$ 1X.\cdots\cdots $,则向右规格化一次,阶码加$ 1 $;
- 若尾数形式为$ 0.\cdots\cdots $,则向左规格化直至变为$ 1.\cdots\cdots $,左移多少位阶码就减多少
溢出判断
- 向右规格化使阶码为全$ 1 $时,发生规格化上溢;
- 向左规格化使阶码为全$ 0 $时,发生规格化下溢;
4.运算器
定点运算器
- 算术逻辑运算单元$ ALU $
- $ n $位$ ALU $包括两个$ n $位的输入操作数$ a $、$ b $,一位进位输入$ C_{in} $,$ AluOp $为运算功能选择操作码,用于选择$ ALU $内部的运算电路;
- 在$ ALU $内部,所有逻辑、算术运算电路并发运行,多个运算结果分别送入多路选择器输入端,由$ AluOp $选择其中一路结果输出;
- 输出除了$ result $外,还包括若干状态标志位:$ CF $、$ ZF $、$ OF $、$ SF $。
- 通用寄存器组
- 作用:暂存参加运算的数据、运算的中间结果或最后结果。
- 输人、输出选择电路
- 作用:对若干个数据的输入、输出进行选择或控制。
- 算术逻辑运算单元$ ALU $
运算器结构
- 单总线结构:$ 2 $个缓冲器,$ 3 $个时钟周期完成运算
- 双总线结构:$ 1 $个缓冲器,$ 2 $个时钟周期完成运算
- 三总线结构:$ 0 $个缓冲器,$ 1 $个时钟周期完成运算
浮点运算器
浮点流水线,将浮点运算的步骤进行细分,优化密集型浮点运算性能